essay on heat transfer

• Why Does Water Expand When It Freezes
• Gold Foil Experiment
• Faraday Cage
• Oil Drop Experiment
• Magnetic Monopole
• Why Do Fireflies Light Up
• Types of Blood Cells With Their Structure, and Functions
• The Main Parts of a Plant With Their Functions
• Parts of a Flower With Their Structure and Functions
• Parts of a Leaf With Their Structure and Functions
• Why Does Ice Float on Water
• Why Does Oil Float on Water
• How Do Clouds Form
• What Causes Lightning
• How are Diamonds Made
• Types of Meteorites
• Types of Volcanoes
• Types of Rocks

Heat Transfer

Heat transfer refers to the phenomenon in which heat or thermal energy is transferred from one region to another. The movement of atoms, ions, and molecules is responsible for carrying the energy. Heat is transferred from a high-temperature region to a low-temperature region. It can also occur between two thermodynamic systems at different temperatures, resulting in changes in internal energies.

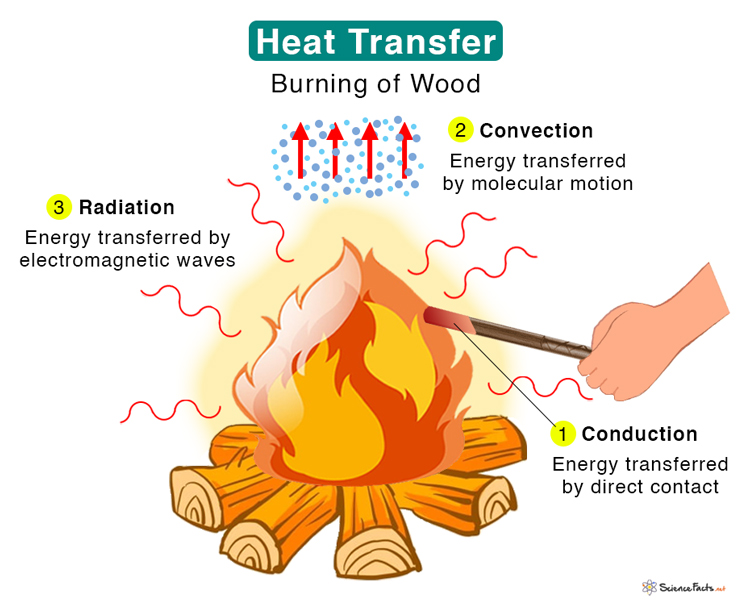
Types of Heat Transfer

Three types of heat transfer occur in nature – conduction , convection , and thermal radiation .

1. Conduction

Heat is transferred between two atoms or molecules in direct contact. The transfer occurs when agitated molecules at high temperatures strike slower molecules at low temperatures, resulting in collisions. Heat transfer occurs through vibrations if the atoms are fixed in a lattice. Conduction takes place in solid, liquid, and gas. For example, when we heat one end of a metal rod, the energy quickly transmits to the other.

According to Fourier’s Law for heat conduction, the heat transfer rate is proportional to the negative temperature gradient and the area at right angles to the gradient through which heat flows. Mathematically, the equation is given by

Q: Heat transfer per unit time

K: Thermal conductivity

A: Cross-sectional area of the conductor

\( \frac{\Delta T}{\Delta x} \): Temperature gradient

2. Convection

Energy is transferred through a medium like liquid or gas. Molecules carry the energy due to the motion of the fluid. For example, when we boil water in a pan, the molecules at the bottom get heated first and carry the energy to the top. In nature, we experience convection currents due to hot air close to the ground that expands, rises, and cools down, resulting in a circular movement.

3. Thermal Radiation

Energy is transferred without any contact between the atoms or molecules. Energy in the form of electromagnetic radiation is emitted by a heated body and absorbed by another. A medium is not required for energy to travel. Electromagnetic waves carry thermal energy. For example, Sun emits heat through radiation, and we feel its warmth.

The intensity of radiation depends on the temperature and the surface characteristics. The radiant heat energy emitted per second per unit area by a surface is proportional to the fourth power of its absolute temperature. It is the basis of Stefan-Boltzmann law , which is represented as follows:

P: Radiant heat energy emitted per second

A: Surface area of the object emitting heat

σ: Stephan-Boltzmann constant

T: Temperature of the object

• Heat Transfer – Hyperphysics.phy-astr.gsu.edu
• Principles of Heating and Cooling – Energy.gov
• The Transfer of Heat Energy – Weather.gov
• Heat Transfer – Teachengineering.org

Article was last reviewed on Monday, January 2, 2023

Related articles

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Popular Articles

Join our Newsletter

Fill your E-mail Address

Related Worksheets

• Privacy Policy

© 2024 ( Science Facts ). All rights reserved. Reproduction in whole or in part without permission is prohibited.

1.4 Heat Transfer, Specific Heat, and Calorimetry

Learning objectives.

By the end of this section, you will be able to:

• Explain phenomena involving heat as a form of energy transfer
• Solve problems involving heat transfer

We have seen in previous chapters that energy is one of the fundamental concepts of physics. Heat is a type of energy transfer that is caused by a temperature difference, and it can change the temperature of an object. As we learned earlier in this chapter, heat transfer is the movement of energy from one place or material to another as a result of a difference in temperature. Heat transfer is fundamental to such everyday activities as home heating and cooking, as well as many industrial processes. It also forms a basis for the topics in the remainder of this chapter.

We also introduce the concept of internal energy, which can be increased or decreased by heat transfer. We discuss another way to change the internal energy of a system, namely doing work on it. Thus, we are beginning the study of the relationship of heat and work, which is the basis of engines and refrigerators and the central topic (and origin of the name) of thermodynamics.

Internal Energy and Heat

A thermal system has internal energy , which is the sum of the microscopic energies of the system. This includes thermal energy, which is associated with the mechanical energies of its molecules and which is proportional to the system’s temperature. As we saw earlier in this chapter, if two objects at different temperatures are brought into contact with each other, energy is transferred from the hotter to the colder object until the bodies reach thermal equilibrium (that is, they are at the same temperature). No work is done by either object because no force acts through a distance (as we discussed in Work and Kinetic Energy ). These observations reveal that heat is energy transferred spontaneously due to a temperature difference. Figure 1.9 shows an example of heat transfer.

The meaning of “heat” in physics is different from its ordinary meaning. For example, in conversation, we may say “the heat was unbearable,” but in physics, we would say that the temperature was high. Heat is a form of energy flow, whereas temperature is not. Incidentally, humans are sensitive to heat flow rather than to temperature.

Since heat is a form of energy, its SI unit is the joule (J). Another common unit of energy often used for heat is the calorie (cal), defined as the energy needed to change the temperature of 1.00 g of water by 1.00 ° C 1.00 ° C —specifically, between 14.5 ° C 14.5 ° C and 15.5 ° C 15.5 ° C , since there is a slight temperature dependence. Also commonly used is the kilocalorie (kcal), which is the energy needed to change the temperature of 1.00 kg of water by 1.00 ° C 1.00 ° C . Since mass is most often specified in kilograms, the kilocalorie is convenient. Confusingly, food calories (sometimes called “big calories,” abbreviated Cal) are actually kilocalories, a fact not easily determined from package labeling.

Mechanical Equivalent of Heat

It is also possible to change the temperature of a substance by doing work, which transfers energy into or out of a system. This realization helped establish that heat is a form of energy. James Prescott Joule (1818–1889) performed many experiments to establish the mechanical equivalent of heat — the work needed to produce the same effects as heat transfer . In the units used for these two quantities, the value for this equivalence is

We consider this equation to represent the conversion between two units of energy. (Other numbers that you may see refer to calories defined for temperature ranges other than 14.5 ° C 14.5 ° C to 15.5 ° C 15.5 ° C .)

Figure 1.10 shows one of Joule’s most famous experimental setups for demonstrating that work and heat can produce the same effects and measuring the mechanical equivalent of heat. It helped establish the principle of conservation of energy. Gravitational potential energy ( U ) was converted into kinetic energy ( K ), and then randomized by viscosity and turbulence into increased average kinetic energy of atoms and molecules in the system, producing a temperature increase. Joule’s contributions to thermodynamics were so significant that the SI unit of energy was named after him.

Increasing internal energy by heat transfer gives the same result as increasing it by doing work. Therefore, although a system has a well-defined internal energy, we cannot say that it has a certain “heat content” or “work content.” A well-defined quantity that depends only on the current state of the system, rather than on the history of that system, is known as a state variable . Temperature and internal energy are state variables. To sum up this paragraph, heat and work are not state variables .

Incidentally, increasing the internal energy of a system does not necessarily increase its temperature. As we’ll see in the next section, the temperature does not change when a substance changes from one phase to another. An example is the melting of ice, which can be accomplished by adding heat or by doing frictional work, as when an ice cube is rubbed against a rough surface.

Temperature Change and Heat Capacity

We have noted that heat transfer often causes temperature change. Experiments show that with no phase change and no work done on or by the system, the transferred heat is typically directly proportional to the change in temperature and to the mass of the system, to a good approximation. (Below we show how to handle situations where the approximation is not valid.) The constant of proportionality depends on the substance and its phase, which may be gas, liquid, or solid. We omit discussion of the fourth phase, plasma, because although it is the most common phase in the universe, it is rare and short-lived on Earth.

We can understand the experimental facts by noting that the transferred heat is the change in the internal energy, which is the total energy of the molecules. Under typical conditions, the total kinetic energy of the molecules K total K total is a constant fraction of the internal energy (for reasons and with exceptions that we’ll see in the next chapter). The average kinetic energy of a molecule K ave K ave is proportional to the absolute temperature. Therefore, the change in internal energy of a system is typically proportional to the change in temperature and to the number of molecules, N . Mathematically, Δ U ∝ Δ K total = N K ave ∝ N Δ T Δ U ∝ Δ K total = N K ave ∝ N Δ T The dependence on the substance results in large part from the different masses of atoms and molecules. We are considering its heat capacity in terms of its mass, but as we will see in the next chapter, in some cases, heat capacities per molecule are similar for different substances. The dependence on substance and phase also results from differences in the potential energy associated with interactions between atoms and molecules.

Heat Transfer and Temperature Change

A practical approximation for the relationship between heat transfer and temperature change is:

where Q is the symbol for heat transfer (“quantity of heat”), m is the mass of the substance, and Δ T Δ T is the change in temperature. The symbol c stands for the specific heat (also called “ specific heat capacity ”) and depends on the material and phase. In the SI system, the specific heat is numerically equal to the amount of heat necessary to change the temperature of 1.00 1.00 kg of mass by 1.00 ° C 1.00 ° C . The SI unit for specific heat is J/ ( kg × K ) J/ ( kg × K ) or J/ ( kg × °C ) J/ ( kg × °C ) . (Recall that the temperature change Δ T Δ T is the same in units of kelvin and degrees Celsius.)

Values of specific heat must generally be measured, because there is no simple way to calculate them precisely. Table 1.3 lists representative values of specific heat for various substances. We see from this table that the specific heat of water is five times that of glass and 10 times that of iron, which means that it takes five times as much heat to raise the temperature of water a given amount as for glass, and 10 times as much as for iron. In fact, water has one of the largest specific heats of any material, which is important for sustaining life on Earth.

The specific heats of gases depend on what is maintained constant during the heating—typically either the volume or the pressure. In the table, the first specific heat value for each gas is measured at constant volume, and the second (in parentheses) is measured at constant pressure. We will return to this topic in the chapter on the kinetic theory of gases.

In general, specific heat also depends on temperature. Thus, a precise definition of c for a substance must be given in terms of an infinitesimal change in temperature. To do this, we note that c = 1 m Δ Q Δ T c = 1 m Δ Q Δ T and replace Δ Δ with d :

Except for gases, the temperature and volume dependence of the specific heat of most substances is weak at normal temperatures. Therefore, we will generally take specific heats to be constant at the values given in the table.

Example 1.5

Calculating the required heat.

• Calculate the temperature difference: Δ T = T f − T i = 60.0 ° C . Δ T = T f − T i = 60.0 ° C .
• Calculate the mass of water. Because the density of water is 1000 kg/m 3 1000 kg/m 3 , 1 L of water has a mass of 1 kg, and the mass of 0.250 L of water is m w = 0.250 kg m w = 0.250 kg .
• Calculate the heat transferred to the water. Use the specific heat of water in Table 1.3 : Q w = m w c w Δ T = ( 0.250 kg ) ( 4186 J/kg ° C ) ( 60.0 ° C ) = 62.8 kJ . Q w = m w c w Δ T = ( 0.250 kg ) ( 4186 J/kg ° C ) ( 60.0 ° C ) = 62.8 kJ .
• Calculate the heat transferred to the aluminum. Use the specific heat for aluminum in Table 1.3 : Q Al = m A1 c A1 Δ T = ( 0.500 kg ) ( 900 J/kg ° C ) ( 60.0 ° C ) = 27.0 kJ . Q Al = m A1 c A1 Δ T = ( 0.500 kg ) ( 900 J/kg ° C ) ( 60.0 ° C ) = 27.0 kJ .
• Find the total transferred heat: Q Total = Q W + Q Al = 89.8 kJ . Q Total = Q W + Q Al = 89.8 kJ .

Significance

Example 1.6 illustrates a temperature rise caused by doing work. (The result is the same as if the same amount of energy had been added with a blowtorch instead of mechanically.)

Example 1.6

Calculating the temperature increase from the work done on a substance.

Calculate the temperature increase of 10 kg of brake material with an average specific heat of 800 J/kg · °C 800 J/kg · °C if the material retains 10% of the energy from a 10,000-kg truck descending 75.0 m (in vertical displacement) at a constant speed.

Because the kinetic energy of the truck does not change, conservation of energy tells us the lost potential energy is dissipated, and we assume that 10% of it is transferred to internal energy of the brakes, so take Q = M g h / 10 Q = M g h / 10 . Then we calculate the temperature change from the heat transferred, using

where m is the mass of the brake material. Insert the given values to find

In a common kind of problem, objects at different temperatures are placed in contact with each other but isolated from everything else, and they are allowed to come into equilibrium. A container that prevents heat transfer in or out is called a calorimeter , and the use of a calorimeter to make measurements (typically of heat or specific heat capacity) is called calorimetry .

We will use the term “calorimetry problem” to refer to any problem in which the objects concerned are thermally isolated from their surroundings. An important idea in solving calorimetry problems is that during a heat transfer between objects isolated from their surroundings, the heat gained by the colder object must equal the heat lost by the hotter object, due to conservation of energy:

We express this idea by writing that the sum of the heats equals zero because the heat gained is usually considered positive; the heat lost, negative.

Example 1.7

Calculating the final temperature in calorimetry.

• Use the equation for heat transfer Q = m c Δ T Q = m c Δ T to express the heat transferred from the pan in terms of the mass of the pan, the specific heat of aluminum, the initial temperature of the pan, and the final temperature: Q hot = m A1 c A1 ( T f − 150 ° C ) . Q hot = m A1 c A1 ( T f − 150 ° C ) .
• Express the heat gained by the water in terms of the mass of the water, the specific heat of water, the initial temperature of the water, and the final temperature: Q cold = m w c w ( T f − 20.0 ° C ) . Q cold = m w c w ( T f − 20.0 ° C ) .
• Note that Q hot < 0 Q hot < 0 and Q cold > 0 Q cold > 0 and that as stated above, they must sum to zero: Q cold + Q hot = 0 Q cold = − Q hot m w c w ( T f − 20.0 ° C ) = − m A1 c A1 ( T f − 150 ° C ) . Q cold + Q hot = 0 Q cold = − Q hot m w c w ( T f − 20.0 ° C ) = − m A1 c A1 ( T f − 150 ° C ) .
• Bring all terms involving T f T f on the left hand side and all other terms on the right hand side. Solving for T f , T f , T f = m A1 c A1 ( 150 ° C ) + m w c w ( 20.0 ° C ) m A1 c A1 + m w c w , T f = m A1 c A1 ( 150 ° C ) + m w c w ( 20.0 ° C ) m A1 c A1 + m w c w , and insert the numerical values: T f = ( 0.500 kg ) ( 900 J/kg ° C ) ( 150 ° C ) + ( 0.250 kg ) ( 4186 J/kg ° C ) ( 20.0 ° C ) ( 0.500 kg ) ( 900 J/kg ° C ) + ( 0.250 kg ) ( 4186 J/kg ° C ) = 59.1 ° C . T f = ( 0.500 kg ) ( 900 J/kg ° C ) ( 150 ° C ) + ( 0.250 kg ) ( 4186 J/kg ° C ) ( 20.0 ° C ) ( 0.500 kg ) ( 900 J/kg ° C ) + ( 0.250 kg ) ( 4186 J/kg ° C ) = 59.1 ° C .

Check Your Understanding 1.3

If 25 kJ is necessary to raise the temperature of a rock from 25 °C to 30 ° C, 25 °C to 30 ° C, how much heat is necessary to heat the rock from 45 °C to 50 ° C 45 °C to 50 ° C ?

Example 1.8

Temperature-dependent heat capacity.

We solve this equation for Q by integrating both sides: Q = m ∫ T 1 T 2 c d T . Q = m ∫ T 1 T 2 c d T .

Then we substitute the given values in and evaluate the integral:

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/university-physics-volume-2/pages/1-introduction

• Authors: Samuel J. Ling, William Moebs, Jeff Sanny
• Publisher/website: OpenStax
• Book title: University Physics Volume 2
• Publication date: Oct 6, 2016
• Location: Houston, Texas
• Book URL: https://openstax.org/books/university-physics-volume-2/pages/1-introduction
• Section URL: https://openstax.org/books/university-physics-volume-2/pages/1-4-heat-transfer-specific-heat-and-calorimetry

© Jul 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.