design experimental factorial

Explore Psychology

Psychology Articles, Study Guides, and Resources

What Is a Factorial Design? Definition and Examples

A factorial design is a type of experiment that involves manipulating two or more variables. While simple psychology experiments look at how one independent variable affects one dependent variable, researchers often want to know more about the effects of multiple independent variables. How a Factorial Design Works Let’s take a closer look at how a…

In this article

A factorial design is a type of experiment that involves manipulating two or more variables. While simple psychology experiments look at how one independent variable affects one dependent variable, researchers often want to know more about the effects of multiple independent variables.

How a Factorial Design Works

Let’s take a closer look at how a factorial design might work in a psychology experiment:

• The independent variable is the variable of interest that the experimenter will manipulate.
• The dependent variable is the variable that the researcher then measures.

By doing this, psychologists can see if changing the independent variable results in some type of change in the dependent variable.

For example, imagine that a researcher wants to do an experiment looking at whether sleep deprivation hurts reaction times during a driving test. If she were only to perform the experiment using these variables–the sleep deprivation being the independent variable and the performance on the driving test being the dependent variable–it would be an example of a simple experiment.

However, let’s imagine that she is also interested in learning if sleep deprivation impacts the driving abilities of men and women differently. She has just added a second independent variable of interest (sex of the driver) into her study, which now makes it a factorial design.

Types of Factorial Designs

One common type of experiment is known as a 2×2 factorial design. In this type of study, there are two factors (or independent variables), each with two levels.

The number of digits tells you how many independent variables (IVs) there are in an experiment, while the value of each number tells you how many levels there are for each independent variable.

So, for example, a 4×3 factorial design would involve two independent variables with four levels for one IV and three levels for the other IV.

Advantages of a Factorial Design

One of the big advantages of factorial designs is that they allow researchers to look for interactions between independent variables.

An interaction is a result in which the effects of one experimental manipulation depends upon the experimental manipulation of another independent variable.

Example of a Factorial Design

For example, imagine that researchers want to test the effects of a memory-enhancing drug. Participants are given one of three different drug doses, and then asked to either complete a simple or complex memory task.

The researchers note that the effects of the memory drug are more pronounced with the simple memory tasks, but not as apparent when it comes to the complex tasks. In this 3×2 factorial design, there is an interaction effect between the drug dosage and the complexity of the memory task.

Understanding Variable Effects in Factorial Designs

So if researchers are manipulating two or more independent variables, how exactly do they know which effects are linked to which variables?

“It is true that when two manipulations are operating simultaneously, it is impossible to disentangle their effects completely,” explain authors Breckler, Olson, and Wiggins in their book Social Psychology Alive .

“Nevertheless, the researchers can explore the effects of each independent variable separately by averaging across all levels of the other independent variable . This procedure is called looking at the main effect.”

Examples of Factorial Designs

A university wants to assess the starting salaries of their MBA graduates. The study looks at graduates working in four different employment areas: accounting, management, finance, and marketing.

In addition to looking at the employment sector, the researchers also look at gender. In this example, the employment sector and gender of the graduates are the independent variables, and the starting salaries are the dependent variables. This would be considered a 4×2 factorial design.

Researchers want to determine how the amount of sleep a person gets the night before an exam impacts performance on a math test the next day. But the experimenters also know that many people like to have a cup of coffee (or two) in the morning to help them get going.

So, the researchers decided to look at how the amount of sleep and caffeine influence test performance. 

The researchers then decided to look at three levels of sleep (4 hours, 6 hours, and 8 hours) and only two levels of caffeine consumption (2 cups versus no coffee). In this case, the study is a 3×2 factorial design.

Baker TB, Smith SS, Bolt DM, et al. Implementing clinical research using factorial designs: A primer .  Behav Ther . 2017;48(4):567-580. doi:10.1016/j.beth.2016.12.005

Collins LM, Dziak JJ, Li R. Design of experiments with multiple independent variables: a resource management perspective on complete and reduced factorial designs .  Psychol Methods . 2009;14(3):202-224. doi:10.1037/a0015826

Haerling Adamson K, Prion S. Two-by-two factorial design .  Clin Simul Nurs . 2020;49:90-91. doi:10.1016/j.ecns.2020.06.004

Watkins ER, Newbold A. Factorial designs help to understand how psychological therapy works .  Front Psychiatry . 2020;11:429. doi:10.3389/fpsyt.2020.00429

Editor-in-Chief

Kendra Cherry, MS.Ed., is a writer, editor, psychosocial therapist, and founder of Explore Psychology, an online psychology resource. She is a Senior Writer for Verywell Mind and is the author of the Everything Psychology Book (Adams Media).

Related Articles:

What Is Habituation (Psychology)? Definition and Examples

Habituation involves responding less to a stimulus after you get used to it.

The Robbers Cave Experiment: Realistic Conflict Theory

Psychologist Muzafer Sherif suggested that conflict between groups was the result of competition for limited resources. To put this theory to the test, he conducted a series of experiments that are today referred to as the Robbers Cave Experiment. In this article, learn more about what happened in the Robbers Cave Experiment and the conclusions…

Absolute Threshold: A Definition With Examples

The absolute threshold is the smallest amount of a stimulus that a person can detect 50% of the time. It can involve any of the senses, including hearing, taste, vision, smell, and touch. The term absolute threshold is often used in psychology research yet students are often confused about what it means. Let’s take a…

What Is a Single-Blind Study?

In psychology, a single-blind study is a type of experiment or clinical trial in which the experimenters are aware of which subjects are receiving the treatment or independent variable, but the participants of the study are not. A study in which both the experimenters and participants are unaware of who is receiving the independent variable and…

What Is an Extraneous Variable? Definition and Challenges

An extraneous variable is anything in a psychology experiment other than the independent and dependent variables. The variables can present challenges and introduce errors, so it is important for experiments to control these extraneous factors. Researchers accomplish this by holding the extraneous variables constant across all conditions of the experiment. In this article, learn more about…

What Is Accommodation In Psychology?

In Piaget’s theory of cognitive development, accommodation refers to the process by which people alter their existing schemas or create new schemas as a result of new learning. This is part of the adaptation process. Old schemas may be changed and, in some cases, entirely new schemas may be formed. How Accommodation Works Piaget’s theory…

Full Factorial Design

A full factorial design is a systematic method for investigating the effects and possible interactions of several factors on a response variable. Unlike a fractional factorial design , a full factorial design includes all possible combinations of factor levels.

The goal is to study how various input variables affect an output variable. The input variables in the system are called factors, and the output variable is referred to as the response or target variable.

Factors are the variables believed to influence the target variable. Each factor has at least two levels or settings. These levels are the specific values a factor can take. The aim is to determine if changing the factor levels has a significant impact on the target variable.

Advantages of Full Factorial Design

Comprehensive Analysis: By testing all possible combinations, you get a complete picture of how the factors influence the outcome.

Interactions: A full factorial design allows for the identification of interactions between factors. This means you can not only measure the isolated effect of each factor but also study how factors work together to influence the outcome.

Disadvantages of Full Factorial Design

Resource Intensive: Since all possible combinations must be tested, the design can become very time-consuming and expensive when a large number of factors and levels are involved. The number of experiments and associated costs increase exponentially with the number of factors.

Full Factorial Design Example

Using a full factorial design, we want to determine what influences the friction torque of a bearing. In this case, friction torque is our response variable. Potential factors could be lubrication and temperature. For lubrication, the factor levels could be "oiled" and "greased," and for temperature, the factor levels could be "low," "medium," and "high."

Now, we want to understand the effect of the different levels on the response variable. This is where a full factorial design can help!

Why Do You Need a Full Factorial Design?

Experiments require time and money! Therefore, it's important to keep the number of experiments as low as possible. However, be cautious—if the number of experiments is too small, you risk missing significant effects. This leads us to two key questions:

First: How can you estimate the required number of experiments?

Second: How can a full factorial design help reduce the number of experiments while still providing reliable results?

Statistics made easy

• many illustrative examples
• ideal for exams and theses
• statistics made easy on 412 pages
• 5rd revised edition (April 2024)
• Only 8.99 €

"Super simple written"

"It could not be simpler"

"So many helpful examples"

Cite DATAtab: DATAtab Team (2024). DATAtab: Online Statistics Calculator. DATAtab e.U. Graz, Austria. URL https://datatab.net

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

Lesson 1: introduction to design of experiments, overview section  .

In this course we will pretty much cover the textbook - all of the concepts and designs included. I think we will have plenty of examples to look at and experience to draw from.

Please note: the main topics listed in the syllabus follow the chapters in the book.

A word of advice regarding the analyses. The prerequisite for this course is STAT 501 - Regression Methods and STAT 502 - Analysis of Variance . However, the focus of the course is on the design and not on the analysis. Thus, one can successfully complete this course without these prerequisites, with just STAT 500 - Applied Statistics for instance, but it will require much more work, and for the analysis less appreciation of the subtleties involved. You might say it is more conceptual than it is math oriented.

  Text Reference: Montgomery, D. C. (2019). Design and Analysis of Experiments , 10th Edition, John Wiley & Sons. ISBN 978-1-119-59340-9

What is the Scientific Method? Section  

Do you remember learning about this back in high school or junior high even? What were those steps again?

Decide what phenomenon you wish to investigate. Specify how you can manipulate the factor and hold all other conditions fixed, to insure that these extraneous conditions aren't influencing the response you plan to measure.

Then measure your chosen response variable at several (at least two) settings of the factor under study. If changing the factor causes the phenomenon to change, then you conclude that there is indeed a cause-and-effect relationship at work.

How many factors are involved when you do an experiment? Some say two - perhaps this is a comparative experiment? Perhaps there is a treatment group and a control group? If you have a treatment group and a control group then, in this case, you probably only have one factor with two levels.

How many of you have baked a cake? What are the factors involved to ensure a successful cake? Factors might include preheating the oven, baking time, ingredients, amount of moisture, baking temperature, etc.-- what else? You probably follow a recipe so there are many additional factors that control the ingredients - i.e., a mixture. In other words, someone did the experiment in advance! What parts of the recipe did they vary to make the recipe a success? Probably many factors, temperature and moisture, various ratios of ingredients, and presence or absence of many additives.  Now, should one keep all the factors involved in the experiment at a constant level and just vary one to see what would happen?  This is a strategy that works but is not very efficient.  This is one of the concepts that we will address in this course.

• understand the issues and principles of Design of Experiments (DOE),
• understand experimentation is a process,
• list the guidelines for designing experiments, and
• recognize the key historical figures in DOE.

What is a Factorial Design of an Experiment?

The factorial design of experiment is described with examples in Video 1.

Video 1. Introduction to Factorial Design of Experiment DOE and the Main Effect Calculation Explained Example .

In a Factorial Design of Experiment, all possible combinations of the levels of a factor can be studied against all possible levels of other factors. Therefore, the factorial design of experiments is also called the crossed factor design of experiments . Due to the crossed nature of the levels, the factorial design of experiments can also be called the completely randomized design (CRD) of experiments . Therefore, the proper name for the factorial design of experiments would be completely randomized factorial design of experiments .

In an easy to understand study of human comfort, two levels of the temperature factor (or independent variable), including 0 O F and 75 O F; and two levels of the humidity factor, including 0% and 35% were studied with all possible combinations (Figure 1). Therefore, the four (2X2) possible treatment combinations, and their associated responses from human subjects (experimental units) are provided in Table 1.

Table 1. Data Structure/Layout of a Factorial Design of Experiment

Coding Systems for the Factor Levels in the Factorial Design of Experiment

As the factorial design is primarily used for screening variables, only two levels are enough. Often, coding the levels as (1) low/high, (2) -/+, (3) -1/+1, or (4) 0/1 is more convenient and meaningful than the actual level of the factors, especially for the designs and analyses of the factorial experiments. These coding systems are particularly useful in developing the methods in factorial and fractional factorial design of experiments. Moreover, general formula and methods can only be developed utilizing the coding system. Coding systems are also useful in response surface methodology. Often, coded levels produce smooth, meaningful and easy to understand contour plots and response surfaces. Moreover, especially in complex designs, the coded levels such as the low- and high-level of a factor are easier to understand.

How to graphically represent the design?

An example graphical representation of a factorial design of experiment is provided in Figure 1 .

Figure 1. Factorial Design of Experiments with two levels for each factor (independent variable, x). The response (dependent variable, y) is shown using the solid black circle with the associated response values.

Test Your Knowledge

Understanding main effects.

9.1 Setting Up a Factorial Experiment

Learning objectives.

• Explain why researchers often include multiple independent variables in their studies.
• Define factorial design, and use a factorial design table to represent and interpret simple factorial designs.

Just as it is common for studies in psychology to include multiple levels of a single independent variable (placebo, new drug, old drug), it is also common for them to include multiple independent variables. Schnall and her colleagues studied the effect of both disgust and private body consciousness in the same study. Researchers’ inclusion of multiple independent variables in one experiment is further illustrated by the following actual titles from various professional journals:

• The Effects of Temporal Delay and Orientation on Haptic Object Recognition
• Opening Closed Minds: The Combined Effects of Intergroup Contact and Need for Closure on Prejudice
• Effects of Expectancies and Coping on Pain-Induced Intentions to Smoke
• The Effect of Age and Divided Attention on Spontaneous Recognition
• The Effects of Reduced Food Size and Package Size on the Consumption Behavior of Restrained and Unrestrained Eaters

Just as including multiple levels of a single independent variable allows one to answer more sophisticated research questions, so too does including multiple independent variables in the same experiment. For example, instead of conducting one study on the effect of disgust on moral judgment and another on the effect of private body consciousness on moral judgment, Schnall and colleagues were able to conduct one study that addressed both questions. But including multiple independent variables also allows the researcher to answer questions about whether the effect of one independent variable depends on the level of another. This is referred to as an interaction between the independent variables. Schnall and her colleagues, for example, observed an interaction between disgust and private body consciousness because the effect of disgust depended on whether participants were high or low in private body consciousness. As we will see, interactions are often among the most interesting results in psychological research.

Factorial Designs

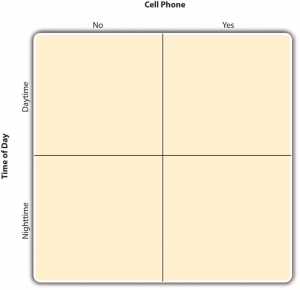
By far the most common approach to including multiple independent variables (which are often called factors) in an experiment is the factorial design. In a  factorial design , each level of one independent variable is combined with each level of the others to produce all possible combinations. Each combination, then, becomes a condition in the experiment. Imagine, for example, an experiment on the effect of cell phone use (yes vs. no) and time of day (day vs. night) on driving ability. This is shown in the  factorial design table  in Figure 9.1. The columns of the table represent cell phone use, and the rows represent time of day. The four cells of the table represent the four possible combinations or conditions: using a cell phone during the day, not using a cell phone during the day, using a cell phone at night, and not using a cell phone at night. This particular design is referred to as a 2 × 2 (read “two-by-two”) factorial design because it combines two variables, each of which has two levels.

If one of the independent variables had a third level (e.g., using a handheld cell phone, using a hands-free cell phone, and not using a cell phone), then it would be a 3 × 2 factorial design, and there would be six distinct conditions. Notice that the number of possible conditions is the product of the numbers of levels. A 2 × 2 factorial design has four conditions, a 3 × 2 factorial design has six conditions, a 4 × 5 factorial design would have 20 conditions, and so on. Also notice that each number in the notation represents one factor, one independent variable. So by looking at how many numbers are in the notation, you can determine how many independent variables there are in the experiment. 2 x 2, 3 x 3, and 2 x 3 designs all have two numbers in the notation and therefore all have two independent variables. The numerical value of each of the numbers represents the number of levels of each independent variable. A 2 means that the independent variable has two levels, a 3 means that the independent variable has three levels, a 4 means it has four levels, etc. To illustrate a 3 x 3 design has two independent variables, each with three levels, while a 2 x 2 x 2 design has three independent variables, each with two levels.

Figure 9.1 Factorial Design Table Representing a 2 × 2 Factorial Design

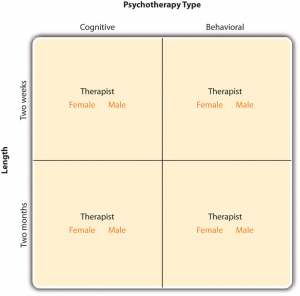
In principle, factorial designs can include any number of independent variables with any number of levels. For example, an experiment could include the type of psychotherapy (cognitive vs. behavioral), the length of the psychotherapy (2 weeks vs. 2 months), and the sex of the psychotherapist (female vs. male). This would be a 2 × 2 × 2 factorial design and would have eight conditions. Figure 9.2 shows one way to represent this design. In practice, it is unusual for there to be more than three independent variables with more than two or three levels each. This is for at least two reasons: For one, the number of conditions can quickly become unmanageable. For example, adding a fourth independent variable with three levels (e.g., therapist experience: low vs. medium vs. high) to the current example would make it a 2 × 2 × 2 × 3 factorial design with 24 distinct conditions. Second, the number of participants required to populate all of these conditions (while maintaining a reasonable ability to detect a real underlying effect) can render the design unfeasible (for more information, see the discussion about the importance of adequate statistical power in Chapter 13). As a result, in the remainder of this section, we will focus on designs with two independent variables. The general principles discussed here extend in a straightforward way to more complex factorial designs.

Figure 9.2 Factorial Design Table Representing a 2 × 2 × 2 Factorial Design

Assigning Participants to Conditions

Recall that in a simple between-subjects design, each participant is tested in only one condition. In a simple within-subjects design, each participant is tested in all conditions. In a factorial experiment, the decision to take the between-subjects or within-subjects approach must be made separately for each independent variable. In a  between-subjects factorial design , all of the independent variables are manipulated between subjects. For example, all participants could be tested either while using a cell phone  or  while not using a cell phone and either during the day  or  during the night. This would mean that each participant would be tested in one and only one condition. In a within-subjects factorial design, all of the independent variables are manipulated within subjects. All participants could be tested both while using a cell phone and  while not using a cell phone and both during the day  and  during the night. This would mean that each participant would need to be tested in all four conditions. The advantages and disadvantages of these two approaches are the same as those discussed in Chapter 5. The between-subjects design is conceptually simpler, avoids order/carryover effects, and minimizes the time and effort of each participant. The within-subjects design is more efficient for the researcher and controls extraneous participant variables.

Since factorial designs have more than one independent variable, it is also possible to manipulate one independent variable between subjects and another within subjects. This is called a  mixed factorial design . For example, a researcher might choose to treat cell phone use as a within-subjects factor by testing the same participants both while using a cell phone and while not using a cell phone (while counterbalancing the order of these two conditions). But he or she might choose to treat time of day as a between-subjects factor by testing each participant either during the day or during the night (perhaps because this only requires them to come in for testing once). Thus each participant in this mixed design would be tested in two of the four conditions.

Regardless of whether the design is between subjects, within subjects, or mixed, the actual assignment of participants to conditions or orders of conditions is typically done randomly.

Non-Manipulated Independent Variables

In many factorial designs, one of the independent variables is a non-manipulated independent variable . The researcher measures it but does not manipulate it. The study by Schnall and colleagues is a good example. One independent variable was disgust, which the researchers manipulated by testing participants in a clean room or a messy room. The other was private body consciousness, a participant variable which the researchers simply measured. Another example is a study by Halle Brown and colleagues in which participants were exposed to several words that they were later asked to recall (Brown, Kosslyn, Delamater, Fama, & Barsky, 1999) [1] . The manipulated independent variable was the type of word. Some were negative health-related words (e.g.,  tumor, coronary ), and others were not health related (e.g.,  election, geometry ). The non-manipulated independent variable was whether participants were high or low in hypochondriasis (excessive concern with ordinary bodily symptoms). The result of this study was that the participants high in hypochondriasis were better than those low in hypochondriasis at recalling the health-related words, but they were no better at recalling the non-health-related words.

Such studies are extremely common, and there are several points worth making about them. First, non-manipulated independent variables are usually participant variables (private body consciousness, hypochondriasis, self-esteem, gender, and so on), and as such, they are by definition between-subjects factors. For example, people are either low in hypochondriasis or high in hypochondriasis; they cannot be tested in both of these conditions. Second, such studies are generally considered to be experiments as long as at least one independent variable is manipulated, regardless of how many non-manipulated independent variables are included. Third, it is important to remember that causal conclusions can only be drawn about the manipulated independent variable. For example, Schnall and her colleagues were justified in concluding that disgust affected the harshness of their participants’ moral judgments because they manipulated that variable and randomly assigned participants to the clean or messy room. But they would not have been justified in concluding that participants’ private body consciousness affected the harshness of their participants’ moral judgments because they did not manipulate that variable. It could be, for example, that having a strict moral code and a heightened awareness of one’s body are both caused by some third variable (e.g., neuroticism). Thus it is important to be aware of which variables in a study are manipulated and which are not.

Non-Experimental Studies With Factorial Designs

Thus far we have seen that factorial experiments can include manipulated independent variables or a combination of manipulated and non-manipulated independent variables. But factorial designs can also include  only non-manipulated independent variables, in which case they are no longer experiments but are instead non-experimental (cross-sectional) in nature. Consider a hypothetical study in which a researcher simply measures both the moods and the self-esteem of several participants—categorizing them as having either a positive or negative mood and as being either high or low in self-esteem—along with their willingness to have unprotected sexual intercourse. This can be conceptualized as a 2 × 2 factorial design with mood (positive vs. negative) and self-esteem (high vs. low) as non-manipulated between-subjects factors. Willingness to have unprotected sex is the dependent variable.

Again, because neither independent variable in this example was manipulated, it is a cross-sectional study rather than an experiment. (The similar study by MacDonald and Martineau [2002] [2]  was an experiment because they manipulated their participants’ moods.) This is important because, as always, one must be cautious about inferring causality from non-experimental studies because of the directionality and third-variable problems. For example, an effect of participants’ moods on their willingness to have unprotected sex might be caused by any other variable that happens to be correlated with their moods.

Key Takeaways

• Researchers often include multiple independent variables in their experiments. The most common approach is the factorial design, in which each level of one independent variable is combined with each level of the others to create all possible conditions.
• Each independent variable can be manipulated between-subjects or within-subjects.
• Non-manipulated independent variables (gender) can be included in factorial designs, however, they limit the causal conclusions that can be made about the effects of the non-manipulated variable on the dependent variable.
• Practice: Return to the five article titles presented at the beginning of this section. For each one, identify the independent variables and the dependent variable.
• Practice: Create a factorial design table for an experiment on the effects of room temperature and noise level on performance on the MCAT. Be sure to indicate whether each independent variable will be manipulated between-subjects or within-subjects and explain why.
• Brown, H. D., Kosslyn, S. M., Delamater, B., Fama, A., & Barsky, A. J. (1999). Perceptual and memory biases for health-related information in hypochondriacal individuals. Journal of Psychosomatic Research, 47 , 67–78. ↵
• MacDonald, T. K., & Martineau, A. M. (2002). Self-esteem, mood, and intentions to use condoms: When does low self-esteem lead to risky health behaviors? Journal of Experimental Social Psychology, 38 , 299–306. ↵

Share This Book

• Increase Font Size

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Factorial Designs

41 setting up a factorial experiment, learning objectives.

• Explain why researchers often include multiple independent variables in their studies.
• Define factorial design, and use a factorial design table to represent and interpret simple factorial designs.

Just as it is common for studies in psychology to include multiple levels of a single independent variable (placebo, new drug, old drug), it is also common for them to include multiple independent variables. Schnall and her colleagues studied the effect of both disgust and private body consciousness in the same study. Researchers’ inclusion of multiple independent variables in one experiment is further illustrated by the following actual titles from various professional journals:

• The Effects of Temporal Delay and Orientation on Haptic Object Recognition
• Opening Closed Minds: The Combined Effects of Intergroup Contact and Need for Closure on Prejudice
• Effects of Expectancies and Coping on Pain-Induced Intentions to Smoke
• The Effect of Age and Divided Attention on Spontaneous Recognition
• The Effects of Reduced Food Size and Package Size on the Consumption Behavior of Restrained and Unrestrained Eaters

Just as including multiple levels of a single independent variable allows one to answer more sophisticated research questions, so too does including multiple independent variables in the same experiment. For example, instead of conducting one study on the effect of disgust on moral judgment and another on the effect of private body consciousness on moral judgment, Schnall and colleagues were able to conduct one study that addressed both questions. But including multiple independent variables also allows the researcher to answer questions about whether the effect of one independent variable depends on the level of another. This is referred to as an interaction between the independent variables. Schnall and her colleagues, for example, observed an interaction between disgust and private body consciousness because the effect of disgust depended on whether participants were high or low in private body consciousness. As we will see, interactions are often among the most interesting results in psychological research.

By far the most common approach to including multiple independent variables (which are often called factors) in an experiment is the factorial design. In a  factorial design , each level of one independent variable is combined with each level of the others to produce all possible combinations. Each combination, then, becomes a condition in the experiment. Imagine, for example, an experiment on the effect of cell phone use (yes vs. no) and time of day (day vs. night) on driving ability. This is shown in the  factorial design table  in Figure 9.1. The columns of the table represent cell phone use, and the rows represent time of day. The four cells of the table represent the four possible combinations or conditions: using a cell phone during the day, not using a cell phone during the day, using a cell phone at night, and not using a cell phone at night. This particular design is referred to as a 2 × 2 (read “two-by-two”) factorial design because it combines two variables, each of which has two levels.

If one of the independent variables had a third level (e.g., using a handheld cell phone, using a hands-free cell phone, and not using a cell phone), then it would be a 3 × 2 factorial design, and there would be six distinct conditions. Notice that the number of possible conditions is the product of the numbers of levels. A 2 × 2 factorial design has four conditions, a 3 × 2 factorial design has six conditions, a 4 × 5 factorial design would have 20 conditions, and so on. Also notice that each number in the notation represents one factor, one independent variable. So by looking at how many numbers are in the notation, you can determine how many independent variables there are in the experiment. 2 x 2, 3 x 3, and 2 x 3 designs all have two numbers in the notation and therefore all have two independent variables. The numerical value of each of the numbers represents the number of levels of each independent variable. A 2 means that the independent variable has two levels, a 3 means that the independent variable has three levels, a 4 means it has four levels, etc. To illustrate a 3 x 3 design has two independent variables, each with three levels, while a 2 x 2 x 2 design has three independent variables, each with two levels.

In principle, factorial designs can include any number of independent variables with any number of levels. For example, an experiment could include the type of psychotherapy (cognitive vs. behavioral), the length of the psychotherapy (2 weeks vs. 2 months), and the sex of the psychotherapist (female vs. male). This would be a 2 × 2 × 2 factorial design and would have eight conditions. Figure 9.2 shows one way to represent this design. In practice, it is unusual for there to be more than three independent variables with more than two or three levels each. This is for at least two reasons: For one, the number of conditions can quickly become unmanageable. For example, adding a fourth independent variable with three levels (e.g., therapist experience: low vs. medium vs. high) to the current example would make it a 2 × 2 × 2 × 3 factorial design with 24 distinct conditions. Second, the number of participants required to populate all of these conditions (while maintaining a reasonable ability to detect a real underlying effect) can render the design unfeasible (for more information, see the discussion about the importance of adequate statistical power in Chapter 13). As a result, in the remainder of this section, we will focus on designs with two independent variables. The general principles discussed here extend in a straightforward way to more complex factorial designs.

Assigning Participants to Conditions

Recall that in a simple between-subjects design, each participant is tested in only one condition. In a simple within-subjects design, each participant is tested in all conditions. In a factorial experiment, the decision to take the between-subjects or within-subjects approach must be made separately for each independent variable. In a  between-subjects factorial design , all of the independent variables are manipulated between subjects. For example, all participants could be tested either while using a cell phone  or  while not using a cell phone and either during the day  or  during the night. This would mean that each participant would be tested in one and only one condition. In a within-subjects factorial design, all of the independent variables are manipulated within subjects. All participants could be tested both while using a cell phone and  while not using a cell phone and both during the day  and  during the night. This would mean that each participant would need to be tested in all four conditions. The advantages and disadvantages of these two approaches are the same as those discussed in Chapter 5. The between-subjects design is conceptually simpler, avoids order/carryover effects, and minimizes the time and effort of each participant. The within-subjects design is more efficient for the researcher and controls extraneous participant variables.

Since factorial designs have more than one independent variable, it is also possible to manipulate one independent variable between subjects and another within subjects. This is called a  mixed factorial design . For example, a researcher might choose to treat cell phone use as a within-subjects factor by testing the same participants both while using a cell phone and while not using a cell phone (while counterbalancing the order of these two conditions). But they might choose to treat time of day as a between-subjects factor by testing each participant either during the day or during the night (perhaps because this only requires them to come in for testing once). Thus each participant in this mixed design would be tested in two of the four conditions.

Regardless of whether the design is between subjects, within subjects, or mixed, the actual assignment of participants to conditions or orders of conditions is typically done randomly.

Non-Manipulated Independent Variables

In many factorial designs, one of the independent variables is a non-manipulated independent variable . The researcher measures it but does not manipulate it. The study by Schnall and colleagues is a good example. One independent variable was disgust, which the researchers manipulated by testing participants in a clean room or a messy room. The other was private body consciousness, a participant variable which the researchers simply measured. Another example is a study by Halle Brown and colleagues in which participants were exposed to several words that they were later asked to recall (Brown, Kosslyn, Delamater, Fama, & Barsky, 1999) [1] . The manipulated independent variable was the type of word. Some were negative health-related words (e.g.,  tumor, coronary ), and others were not health related (e.g.,  election, geometry ). The non-manipulated independent variable was whether participants were high or low in hypochondriasis (excessive concern with ordinary bodily symptoms). The result of this study was that the participants high in hypochondriasis were better than those low in hypochondriasis at recalling the health-related words, but they were no better at recalling the non-health-related words.

Such studies are extremely common, and there are several points worth making about them. First, non-manipulated independent variables are usually participant variables (private body consciousness, hypochondriasis, self-esteem, gender, and so on), and as such, they are by definition between-subjects factors. For example, people are either low in hypochondriasis or high in hypochondriasis; they cannot be tested in both of these conditions. Second, such studies are generally considered to be experiments as long as at least one independent variable is manipulated, regardless of how many non-manipulated independent variables are included. Third, it is important to remember that causal conclusions can only be drawn about the manipulated independent variable. For example, Schnall and her colleagues were justified in concluding that disgust affected the harshness of their participants’ moral judgments because they manipulated that variable and randomly assigned participants to the clean or messy room. But they would not have been justified in concluding that participants’ private body consciousness affected the harshness of their participants’ moral judgments because they did not manipulate that variable. It could be, for example, that having a strict moral code and a heightened awareness of one’s body are both caused by some third variable (e.g., neuroticism). Thus it is important to be aware of which variables in a study are manipulated and which are not.

Non-Experimental Studies With Factorial Designs

Thus far we have seen that factorial experiments can include manipulated independent variables or a combination of manipulated and non-manipulated independent variables. But factorial designs can also include  only non-manipulated independent variables, in which case they are no longer experiments but are instead non-experimental in nature. Consider a hypothetical study in which a researcher simply measures both the moods and the self-esteem of several participants—categorizing them as having either a positive or negative mood and as being either high or low in self-esteem—along with their willingness to have unprotected sexual intercourse. This can be conceptualized as a 2 × 2 factorial design with mood (positive vs. negative) and self-esteem (high vs. low) as non-manipulated between-subjects factors. Willingness to have unprotected sex is the dependent variable.

Again, because neither independent variable in this example was manipulated, it is a non-experimental study rather than an experiment. (The similar study by MacDonald and Martineau [2002] [2]  was an experiment because they manipulated their participants’ moods.) This is important because, as always, one must be cautious about inferring causality from non-experimental studies because of the directionality and third-variable problems. For example, an effect of participants’ moods on their willingness to have unprotected sex might be caused by any other variable that happens to be correlated with their moods.

• Brown, H. D., Kosslyn, S. M., Delamater, B., Fama, A., & Barsky, A. J. (1999). Perceptual and memory biases for health-related information in hypochondriacal individuals. Journal of Psychosomatic Research, 47 , 67–78. ↵
• MacDonald, T. K., & Martineau, A. M. (2002). Self-esteem, mood, and intentions to use condoms: When does low self-esteem lead to risky health behaviors? Journal of Experimental Social Psychology, 38 , 299–306. ↵

Experiments that include more than one independent variable in which each level of one independent variable is combined with each level of the others to produce all possible combinations.

Shows how each level of one independent variable is combined with each level of the others to produce all possible combinations in a factorial design.

All of the independent variables are manipulated between subjects.

A design which manipulates one independent variable between subjects and another within subjects.

An independent variable that is measured but is non-manipulated.

Research Methods in Psychology Copyright © 2019 by Rajiv S. Jhangiani, I-Chant A. Chiang, Carrie Cuttler, & Dana C. Leighton is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Teach yourself statistics

What is a Full Factorial Experiment?

This lesson describes full factorial experiments. Specifically, the lesson answers four questions:

• What is a full factorial experiment?
• What causal effects can we test in a full factorial experiment?
• How should we interpret causal effects?
• What are the advantages and disadvantages of a full factorial experiment?

What is a Factorial Experiment?

A factorial experiment allows researchers to study the joint effect of two or more factors on a dependent variable . Factorial experiments come in two flavors: full factorials and fractional factorials. In this lesson, we will focus on the full factorial experiment, not the fractional factorial.

Full Factorial Experiment

A full factorial experiment includes a treatment group for every combination of factor levels. Therefore, the number of treatment groups is the product of factor levels. For example, consider the full factorial design shown below:

Factor A has two levels, factor B has three levels, and factor C has four levels. Therefore, this full factorial design has 2 x 3 x 4 = 24 treatment groups.

Full factorial designs can be characterized by the number of treatment levels associated with each factor, or by the number of factors in the design. Thus, the design above could be described as a 2 x 3 x 4 design (number of treatment levels) or as a three-factor design (number of factors).

Fractional Factorial Experiments

The other type of factorial experiment is a fractional factorial. Unlike full factorial experiments, which include a treatment group for every combination of factor levels, fractional factorial experiments include only a subset of possible treatment groups.

Causal Effects

A full factorial experiment allows researchers to examine two types of causal effects: main effects and interaction effects. To facilitate the discussion of these effects, we will examine results (mean scores) from three 2 x 2 factorial experiments:

Experiment I: Mean Scores

Experiment II: Mean Scores

Experiment III: Mean Scores

Main Effects

In a full factorial experiment, a main effect is the effect of one factor on a dependent variable, averaged over all levels of other factors. A two-factor factorial experiment will have two main effects; a three-factor factorial, three main effects; a four-factor factorial, four main effects; and so on.

How to Measure Main Effects

To illustrate what is going on with main effects, let's look more closely at the main effects from Experiment I:

Assuming there were an equal number of observations in each treatment group, we can compute the main effect for Factor A as shown below:

Effect of A at level B 1 = A 2 B 1 - A 1 B 1 = 2 - 5 = -3

Effect of A at level B 2 = A 2 B 2 - A 1 B 2 = 5 - 2 = +3

Main effect of A = ( -3 + 3 ) / 2 = 0

And we can compute the main effect for Factor B as shown below:

Effect of B at level A 1 = A 1 B 2 - A 1 B 1 = 5 - 2 = +3

Effect of B at level A 2 = A 2 B 2 - A 2 B 1 = 2 - 5 = -3

Main effect of B = ( 3 - 3 ) / 2 = 0

In a similar fashion, we can compute main effects for Experiment II (see Problem 1 ) and Experiment III (see Problem 2 ).

Warning: In a full factorial experiment, you should not attempt to interpret main effects until you have looked at interaction effects. With that in mind, let's look at interaction effects for Experiments I, II, and III.

Interaction Effects

In a full factorial experiment, an interaction effect exists when the effect of one independent variable depends on the level of another independent variable.

When Interactions Are Present

The presence of an interaction can often be discerned when factorial data are plotted. For example, the charts below plot mean scores from Experiment I and from Experiment II:

Experiment I

Experiment II

In Experiment I, consider how the dependent variable score is affected by level A1 versus level A2. In the presence of B1, the dependent variable score is bigger for A1 than for A2. But in the presense of B2, the reverse is true - the dependent variable score is bigger for A2 than for A1.

In Experiment II, level C1 is associated with a little bit bigger dependent variable score in the presence of D1; but a much bigger dependent variable score in the presence of D2.

In both charts, the way that one factor affects the dependent variable depends on the level of another factor. This is the definition of an interaction effect. In charts like these, the presence of an interaction is indicated by non-parallel plotted lines.

Note: These charts are called interaction plots. For guidance on creating and interpreting interaction plots, see Interaction Plots .

When Interactions Are Absent

Now, look at the chart below, which plots mean scores from Experiment III:

Experiment III

In this chart, E1 has the same effect on the dependent variable, regardless of the level of Factor F. At each level of Factor F, the dependent variable is 2 units bigger with E1 than with E2. So, in this chart, there is no interaction between Factors E and F. And you can tell at a glance that there is no interaction, because the plotted lines are parallel.

Number of Interactions

The number of interaction effects in a full factorial experiment is determined by the number of factors. A two-factor design (with factors A and B) has one two-way interaction (the AB interaction). A three-factor design (with factors A, B, and C) has one three-way interaction (the ABC interaction) and three two-way interactions (the AB, AC, and BC interactions).

A general formula for finding the number of interaction effects (NIE) in a full factorial experiment is:

where k C r is the number of combinations of k things taken r at a time, k is the number of factors in the full factorial experiment, and r is the number of factors in the interaction term.

Note: If you are unfamiliar with combinations, see Combinations and Permutations .

How to Interpret Causal Effects

Recall that the purpose of conducting a full factorial experiment is to understand the joint effects (main effects and interaction effects) of two or more independent variables on a dependent variable. When a researcher looks at actual data from an experiment, small differences in group means are expected, even when independent variables have no causal connection to the dependent variable. These small differences might be attributable to random effects of unmeasured extraneous variables .

So the real question becomes: Are observed effects significantly bigger than would be expected by chance - big enough to be attributable to a main or interaction effect rather than to an extraneous variable? One way to answer this question is with analysis of variance. Analysis of variance will test all main effects and interaction effects for statistical significance. Here is how to interpret the results of that test:

• If no effects (main effects or interaction effects) are statistically significant, conclude that the independent variables do not affect the dependent variable.
• If a main effect is statistically significant, conclude that the main effect does affect the dependent variable.
• If an interaction effect is statistically significant, conclude that the interaction factors act in combination to affect the dependent variable.

Recognize that it is possible for factors to affect the dependent variable, even when the main effects are not statistically significant. We saw an example of that in Experiment I.

In Experiment I, both main effects were zero; yet, the interaction effect is dramatic. The moral here is: Do not attempt to interpret main effects until you have looked at interaction effects.

Note: To learn how to implement analysis of variance for a full factorial experiment, see ANOVA With Full Factorial Experiments .

Advantages and Disadvantages

Analysis of variance with a full factorial experiment has advantages and disadvantages. Advantages include the following:

• The design permits a researcher to examine multiple factors in a single experiment.
• The design permits a researcher to examine all interaction effects.
• The design requires subjects to participate in only one treatment group.

Disadvantages include the following:

• When the experiment includes many factors and levels, sample size requirements may be excessive.
• The need to include all treatment combinations, regardless of importance, may waste resources.

Test Your Understanding

The table below shows results from a 2 x 2 factorial experiment.

Assuming equal sample size in each treatment group, what is the main effect for both factors?

(A) -2 (B) 3.5 (C) 4 (D) 7 (E) 14

The correct answer is (A). We can compute the main effect for Factor C as shown below:

Effect of C at level D 1 = C 2 D 1 - C 1 D 1 = 4 - 5 = -1

Effect of C at level D 2 = C 2 D 2 - C 1 D 2 = 1 - 4 = -3

Main effect of C = ( -1 + -3 ) / 2 = -2

And we can compute the main effect for Factor D as shown below:

Effect of D at level C 1 = C 1 D 2 - C 1 D 1 = 4 - 5 = -1

Effect of D at level C 2 = C 2 D 2 - C 2 D 1 = 1 - 4 = -3

Main effect of D = ( -1 + -3 ) / 2 = -2

(A) -12 (B) -2 (C) 0 (D) 3 (E) 4

The correct answer is (B). We can compute the main effect for Factor E as shown below:

Effect of E at level F 1 = E 2 F 1 - E 1 F 1 = 3 - 5 = -2

Effect of E at level F 2 = E 2 F 2 - E 1 F 2 = 1 - 3 = -2

Main effect of E = ( -2 + -2 ) / 2 = -2

And we can compute the main effect for Factor F as shown below:

Effect of F at level C 1 = E 1 F 2 - E 1 F 1 = 3 - 5 = -2

Effect of F at level C 2 = E 2 F 2 - E 2 F 1 = 1 - 3 = -2

Main effect of F = ( -2 + -2 ) / 2 = -2

Consider the interaction plot shown below. Which of the following statements are true?

(A) There is a non-zero interaction between Factors A and B. (B) There is zero interaction between Factors A and B. (C) The plot provides insufficient information to describe the interaction.

The correct answer is (B). At every level of Factor B, the difference between A1 and A2 is 3 units. Because the effect of Factor A is constant (always 3 units) at every level of Factor B, there is no interaction between Factors A and B.

Note: The parallel pattern of lines in the interaction plot indicates that the AB interaction is zero.

Factorial Design

• Reference work entry
• pp 2144–2145
• Cite this reference work entry

• David Nordstokke 3 &
• S. Mitchell Colp 3  

1701 Accesses

3 Citations

Experimental design ; Multifactor design ; Randomized clinical trial ; Randomized trial

Factorial design is a type of research methodology that allows for the investigation of the main and interaction effects between two or more independent variables and on one or more outcome variable(s).

Description

It has been argued that factorial designs epitomize the true beginning of modern behavioral research and have caused a significant paradigm shift in the way social scientists conceptualize their research questions and produce objective outcomes (Kerlinger & Lee, 2000 ). Factorial design can be categorized as an experimental methodology which goes beyond common single-variable experimentation. In the past, social scientists had been transfixed on singular independent variable experiments and foreshadowed the importance of extraneous variables which are able to attenuate or diminish research findings. With widespread adoption of factorial design, social scientists could now...

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Subscribe and save.

• Get 10 units per month
• Download Article/Chapter or eBook
• 1 Unit = 1 Article or 1 Chapter
• Cancel anytime
• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Durable hardcover edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Keppel, G., & Wickens, T. D. (2004). Design and analysis: A researcher’s handbook . Newmarket, ON: Pearson.

Google Scholar  

Kerlinger, F. N., & Lee, L. B. (2000). Foundations of behavioral research . Florence, KY: Wadsworth Publishing.

Mee, R. (2009). A comprehensive guide to factorial two-level experimentation . New York: Springer Publishing.

Mukerjee, R., & Wu, C. F. J. (2006). A modern theory of factorial designs . New York: Springer Publishing.

Sattler, J. M. (2004). Assessment of children: Cognitive applications (4th ed.). San Diego: Author.

Download references

Author information

Authors and affiliations.

Educational Studies in School Psychology, University of Calgary, 2500 University Drive NW, Calgary, AB, Canada

David Nordstokke & S. Mitchell Colp

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to David Nordstokke .

Editor information

Editors and affiliations.

University of Northern British Columbia, Prince George, BC, Canada

Alex C. Michalos

(residence), Brandon, MB, Canada

Rights and permissions

Reprints and permissions

Copyright information

© 2014 Springer Science+Business Media Dordrecht

About this entry

Cite this entry.

Nordstokke, D., Colp, S.M. (2014). Factorial Design. In: Michalos, A.C. (eds) Encyclopedia of Quality of Life and Well-Being Research. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-0753-5_982

Download citation

DOI : https://doi.org/10.1007/978-94-007-0753-5_982

Publisher Name : Springer, Dordrecht

Print ISBN : 978-94-007-0752-8

Online ISBN : 978-94-007-0753-5

eBook Packages : Humanities, Social Sciences and Law Reference Module Humanities and Social Sciences Reference Module Business, Economics and Social Sciences

Share this entry

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research