what is newton's ring experiment

• Why Does Water Expand When It Freezes
• Gold Foil Experiment
• Faraday Cage
• Oil Drop Experiment
• Magnetic Monopole
• Why Do Fireflies Light Up
• Types of Blood Cells With Their Structure, and Functions
• The Main Parts of a Plant With Their Functions
• Parts of a Flower With Their Structure and Functions
• Parts of a Leaf With Their Structure and Functions
• Why Does Ice Float on Water
• Why Does Oil Float on Water
• How Do Clouds Form
• What Causes Lightning
• How are Diamonds Made
• Types of Meteorites
• Types of Volcanoes
• Types of Rocks

Newton’s Rings

Definition: what are newton’s rings.

Newton’s rings are a series of concentric circular rings consisting of bright- and dark-colored fringes. When a plano-convex lens lies on top of a plane lens or glass sheet, a small layer of air is formed between the two lenses. Newton’s rings are formed by the interference phenomenon when monochromatic and coherent rays of light are reflected from the top and bottom surfaces of this air film. The film’s thickness varies from zero at the point of contact to a finite value in the wedge -shaped region.

By studying the pattern of concentric rings, it is possible to determine the wavelength of monochromatic light and the refractive index of a given transparent liquid medium present in a wedge-shaped film. If white light is used instead of monochromatic, the lens system produces colorful interference, since the condition for a maximum in the interference is dependent on the wavelength.

Newton’s rings have been named after English physicist and mathematician Sir Isaac Newton, who was the first to observe the effect in 1704.

Principle of Newton’s Rings Formation

The phenomenon of the formation of Newton’s rings can be explained based on the wave theory of light.

• An air film of varying thickness is formed between the lens and the glass sheet.
• When a ray falls on the surface of the lens, it is reflected as well as refracted.
• When the refracted ray strikes the glass sheet, it undergoes a phase change of 180° on reflection .
• Interference occurs between two waves that interfere constructively if the path difference between them is (m+1/2)λ and destructively if the path difference between them is mλ, thereby producing alternate bright and dark rings.

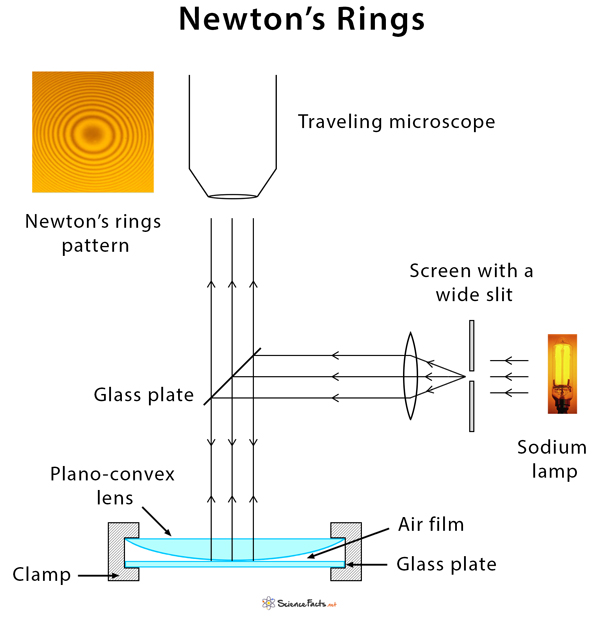
Newton’s Rings Experiment

The apparatus consists of the following components.

• Nearly monochromatic source of light (sodium light)
• Plano-convex lens
• Optically flat glass plates
• Convex lens
• Traveling microscope

The experimental setup for Newton’s ring is shown in the figure above. The convex surface of a plano-convex lens having a long focal length (large radius of curvature) is placed in contact with a plane glass plate and clamped together. Light from a monochromatic source (e.g., sodium lamp) is allowed to fall on a convex lens through a wide slit, which renders it into a nearly parallel beam. At first, light falls on a glass plate inclined at an angle of 45° to the vertical before reaching the lens-plate system at the bottom. Light is reflected from the upper surface of the glass plate and the lower surface of the lens. Due to the air film formed by the glass plate and lens, interference fringes are formed, which are observed directly through a traveling microscope. The rings are concentric circles. A dark central spot is obtained when viewed by reflection.

Theory and Equations

Consider a ray of light incident on the air film at a point where its thickness is t . The optical path difference between the two reflected rays will be 2t . Taking into account the phase change of 180° for reflection at the rare to the dense surface, the conditions for constructive and destructive interference are

                      2t = (m+1/2) λ (for constructive interference or bright rings)

                                  2t = (m+1/2) λ (for destructive interference or dark rings)

where m is the order of the ring and can take the values m = 0, 1, 2, 3, …, n

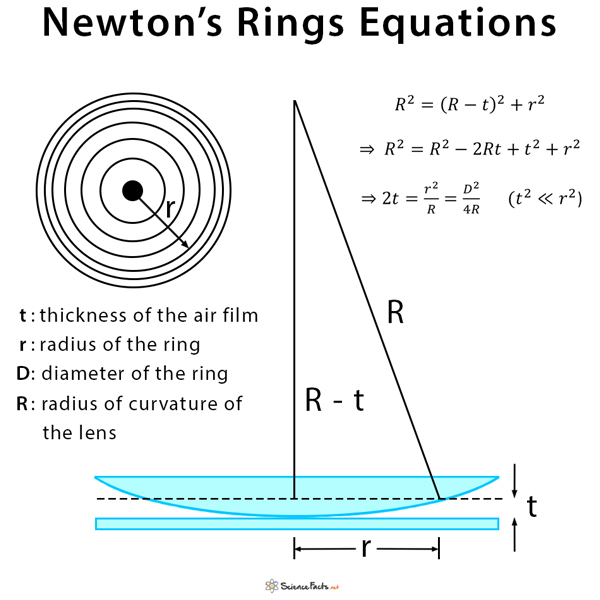
If R is the radius of curvature of the lens and r is the distance of the point under consideration to the point of contact of the lens and glass plate, then

R 2 = (R-t) 2 + r 2

or, R 2 = R 2 – 2Rt + t 2 + r 2

or, 2t = r 2 /R = D 2 /4R

since t 2 << r 2 and D = 2r , the diameter of a ring.

Combine this result with the condition for the m th and n th dark rings. Then, the diameters of the two rings are given by

D m 2 = 4Rmλ

D n 2 = 4Rnλ

Subtracting the two equations and rearranging

D n 2 – D m 2  = 4R(n-m)λ

λ = (D n 2 – D m 2 )/4R(n-m)  

Thus, the wavelength λ can be determined from this equation.

If a liquid of refractive index μ is introduced between the lens and the plate, then the path difference is given by 2μt . The diameter of any ring will be less with the liquid in place than without it. The equation for wavelength is given by

λ = (D n 2 – D m 2 )μ/4R(n-m)  

In a laboratory experiment, students are required to calculate the radius of curvature R of the lens. It is calculated by spherometer using the following relation

R = l 2 /6h + h/2

Here, l is the mean length of the three sides of the equilateral triangle formed by joining the tips of three outer legs, and h represents the height of the central screw above or below the plane of the outer legs.

Image courtesy: Softsolder.com

Newton’s Rings Video

Newton’s rings in transmitted light.

Newton’s rings are studied in transmitted light as well. The interference conditions for reflection and transmitted light are complementary. The diameters of the bright rings calculated for transmitted light using the equations above correspond precisely to the diameters of the dark rings in reflection. In particular, the center of Newton’s rings is bright in transmitted light and dark in reflection.

Applications of Newton’s Rings

Newton’s rings are a phenomenon that can be viewed daily. Some of its applications are as follows.

• For testing the uniformity of a polished surface by studying the interference pattern the surface makes when placed in contact with a perfectly flat glass surface
• To control the thickness of paint that is used on posters. Too much paint would exceed total weight requirements, and too little would result in faint imprints.

Ans. The plano-convex lens is circular. All the bright and dark fringes are the loci of the points of the film of equal thickness. As the equally thick films are formed along the diameter of the circular shape, the fringe pattern is also circular.

Ans. At the point of contact of the lens with the glass plate, the thickness of the air film is minimal compared to the wavelength of light. Therefore, the path difference introduced between the interfering waves is zero, the condition of minimum intensity. Consequently, the interfering waves at the center are opposite in phase and interfere destructively.

Ans. Sodium light is used in Newton’s rings experiment because it is monochromatic, and the two spectral lines of sodium can be resolved without difficulty.

• Interference: Newton’s Rings – Animations.physics.unsw.edu.au
• Laboratory Manual for Newton’s Rings Method – Nitj.ac.in
• Newton’s Rings – Iiserpune.ac.in
• Newton’s Rings: Wavelength of Light – Vlab.amrita.edu
• Newton’s Rings – Iitr.ac.in
• Newton’s Rings – Sciencedemonstrations.fas.harvard.edu
• Demonstrations in Optics : Newton’s Rings – Physicsed.buffalostate.edu
• Newton’s Rings Experiment – Brainkart.com
• Newton’s Rings – Niser.ac.in
• Investigation of Interference Patterns and Newton’s Rings- Slideshare.net

Article was last reviewed on Friday, February 3, 2023

Related articles

3 responses to “Newton’s Rings”

The diagram may be mislabeled. Perhaps R and RT are the wrong way around.

Thank you for your comment. We have edited the image.

this content is very nice,very useful for me and thank u so much

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Popular Articles

Join our Newsletter

Fill your E-mail Address

Related Worksheets

• Privacy Policy

© 2024 ( Science Facts ). All rights reserved. Reproduction in whole or in part without permission is prohibited.

An extended interference pattern is most easily seen using light with only a very narrow band of wavelengths. Here we use a sodium vapour lamp, in the box at left in this photo. The lens geometry is sketched below.

The geometry and the interference pattern

The sketch at left shows the global geometry. The convex side of the lens has a radius of curvature R and we consider one of the rigns with radius r where the air film between lens and flat has thickness t . We analyse this geometry below.

At right we see a photograph of the interference pattern. The large dark patch at the centre is around the point where the convex lens surface touches the glass flat below it. In this area, the thin film of air between the lens and the flat has a thickness much less than the wavelength of light. This is surrounded by bright and dark circles, due to constructive and destructive interference respectively.

Reflections and the conditions for constructive and destructive interference

This sketch shows the geometry close to the point* of contact between the convext lens (top) and glass flat (bottom). The other surfaces (the top surface of the lens and the bottom surface of the flat) are assumed to be so far away that reflections from them don't produce interference fringes: see Coherence length .

Consider first the arrows closest to the point of contact, where the separation t between interfaces is rather less than a quarter wavelength, λ /4. Now consider the reflection from the top surface and that from the bottom: the two parallel rays travelling upwards. The component of phase difference between these two that is due to their different pathlength, which is much less than π.

Now consider the phase difference due to reflections. (See Reflections and phases for an introduction.) At the upper surface, the ray reflects going from glass towards air – high n to low n – so the phase change is zero, as indicated on the sketch. At the lower surface, the ray reflects going from air towards glass – low n to high – so the phase change is π. So, with small phase change due to path length but a π phase change due to the two reflections, these two rays are about π radians or half of one cycle out of phase, which gives destructive interference. Consequence: in this region close to the point of contact, there is destructive interference in reflection .

Next consider the middle set of rays in the sketch. Here the thickness is t = λ /4, so the path difference is 2 t = λ /2. This gives a phase difference of π. Add this to the π from the reflections and the phase difference is 2π – the two rays are out of phase by one complete cycle. So, provided the coherence length is sufficiently long, these rays give constructive interference in reflection .

Finally, the rays in the sketch at left are for an air film thickness of t = λ /2, so the path difference is 2 t = λ . This gives a phase difference of 2π. Add this to the π from the reflections and the phase difference is 3π – the two rays are out of phase by one and a half complete cycles. This time we have destructive interference in reflection .

And so on: our thin film has a varying thickness, so we have different interference conditions at different thicknesses. This leads to the alternating rings of constructive interference (bright rings) and destructive interference (dark), as shown in the photograph. We can use these rings to determine the radius of curvature of the lens surface, as shown below. But first, let's stop to think about:

Newton's rings in transmission

The radius of the rings gives the radius of curvature of the lens.

Let's consider a dark ring with radius r at a point where the separation is t . The right angled triangle shown in red has a height R–t so Pythagoras' theorem gives us

Talk to our experts

1800-120-456-456

• Newton's Rings

Introduction to Newton’s Rings

A Ring of Newton's is an Optical phenomenon that appears as a Ring of dark-colored lights or bands when one piece of glass is Convex and rests on another piece of flat glass. Therefore, there is space between them that is filled with air. Light waves are said to cause this phenomenon as their interference results in a brightening of light when their crests coincide, but the opposite occurs when the crest meets the trough. This is described as the destruction of light. During the transmission of light between the two pieces of glass, waves from both the top and bottom surfaces of the air film interfere with each other. This section will present all the information related to Newton's Ring. Newton was the first Physicist to investigate the Rings quantitatively, and he is credited with naming them after him.

What are Newton's Rings?

It is said that Newton's Rings are formed by the interference pattern between two surfaces caused by the light reflecting between them. There are two flat surfaces on either side of the sphere. In 1704, Isaac Newton described the effect in a treatise called Opticks based on his research. Newton's Rings are visible when viewed with monochromatic light as alternating bright and dark circles located at the point of contact between the two surfaces. The different wavelengths of light conflict at very different levels of thickness in the layer of air between the two surfaces when viewed in white light . This results in a pattern of a concentric circle of Rainbow colors.

An Optical glass that has a flat surface is placed on a very slightly curved Convex glass to create the pattern. At other points, there is a slight air gap between the two surfaces of the two pieces of glass which are in contact only at the center. The increasing distance between the center and the microscope is referred to as the radial distance. On the right side of one of the pieces, there is a small gap growing from left to right. In the monochromatic example, the source of color is a monochromatic single source of light shining through the top piece and refracting off the bottom and top surfaces. In the resulting superposition, the two rays are combined. 

This ray, however, generally travels a relatively long path as it reflects off the surface of the bottom. Two times the gap between the surfaces equals the additional path length.

A 180° phase reverse happens when the ray reflects off the bottom piece of glass. As a result, the phase reversal due to the internal reflection of the other ray from the underside of the top glass does not occur.

Formation of Newton’s Rings

Light waves are interfered with to create Newton's Rings when Reflections occur between the top and bottom surfaces of the air film formed between the lens and glass sheet.

According to the theory of waves of light, the formation of Rings of Newton's can be explained as follows:

In between the glass sheet and lens is an air film of varying thickness.

Reflection and refractive rays occur simultaneously when a ray strikes the lens surface.

Rays that are refracted have a phase change of 180 on the reflection when they strike a glass sheet.

If the path difference between two waves is m+ 1 / 2 *1, an interference happens constructively, while destructively if the path difference between them is ml. This produces alternate bright and dark Rings.

FAQs on Newton's Rings

1. What are Newton's Rings and How They are Formed?

The rings of Newton's are formed as a result of interference which is between the light waves that are reflected from the top and bottom surfaces of the air film which is formed between the lens and glass sheet. A film of air which is of varying thickness is formed between the lens and the glass sheet.

2. Why Newton's Rings Circular?

The path of difference between the ray that is reflected and the ray which is the incident depends upon the thickness of the air gap between the lens and the base. As the lens is said to be symmetric along its axis the thickness is said to be constant along the circumference which is of a ring of a given radius. Hence we see that Newton's rings are circular.

3. Explain What the Newton Ring Experiment is.

The apparatus for Newton's ring and the aim of the experiment are to study the formation of Newton's rings in the air-film in between a lens which is a plano-convex and a glass plate by using a nearly monochromatic light from a sodium-source and hence this is to determine the radius of curvature of the plano-convex lens.

4. What are the Applications of Newton's Ring?

FRED generally is said to be allowed for simulation of physical optics phenomena such as diffraction and interference. With this capability, the components such as the Gaussian beam of laser and interferometers can be accurately modeled and incorporated into a system that is optical.

(Image will be Updated soon)

5. How did Newton's Rings get its dark central fringe?

Newton's Rings are formed by interference between thin films of uniformly increasing thickness on either side of a bright or dark central circle. A film of air is present between the lens and the glass, but there is reflection coming from the denser medium at the lower surface of the film. As a result, the path difference is λ/2. Therefore, the center of the image has a dark fringe.

6. Why Newton's Rings lit by Monochromatic light?

When monochromatic light is used there is no doubt about the interference pattern. Because different wavelengths of light interfere at different thicknesses, white light will not produce a clear interference pattern.

7. In Newton's Ring, what is a backlash error?

Play in the screw increases with use or as a result of wear and tear, such that when it is rotated in a particular direction the screw slips into the nut and no linear distance is covered for certain rotations of the screw head. The error that results from this is known as a backlash error.

4. Why are Newton's Rings circular?

Depending on the thickness of the air gap between the lens and the base, the path of difference between the ray that is reflected and the ray which is incident is different. A symmetrical lens will have the same thickness across its axis as it will have along its circumference, as if it were a Ring of given radius. As a consequence, Newton's Rings are Elliptical.

9. Can you explain why the center of Newton's Rings is perfectly black?

Because of the thin air film formed between the glass plate and lens at the center, the central fRinge of Newton's Rings is dark in the reflector system. As a result, the angle of incidence between the incident and reflected rays is equal to zero at the geometrical path.

• Utility Menu

Harvard Natural Sciences Lecture Demonstrations

1 Oxford St Cambridge MA 02138 Science Center B-08A (617) 495-5824

• Key to Catalog

enter search criteria into the search box

Newton's rings, what it shows:.

Waves reflecting from two surfaces can interfere constructively and destructively. In this case it is light waves that are being reflected at glass/air and air/glass interfaces. The interference produces a concentric ring pattern of rainbow colors in white light, or dark and light rings in monochromatic light.

How it works:

Setting it up:.

The entire setup fits very nicely on one of the lecture carts and can be readied beforehand and wheeled out complete. For a uniform white light source, a light box 5 is used. For monochromatic illumination, use the green mercury light box. 6 Place a black felt cloth under the Newton's Rings apparatus and position the color CCD video camera and light source on opposite sides of the apparatus to secure an approximate 45° reflection. The 50 mm Nikon lens with a 5 mm extension ring will nicely frame the small apparatus. The 35" Mitsubishi monitor will give the truest colors; the rear-projection video is pretty good and doesn't use up floor space.

A classic demonstration dating way back to none other than Newton himself. However, his explanation of the rings (light particles undergoing "fits and starts" of easy and difficult reflections) left something to be desired.

1 The metal frame with its three adjusting screws (not shown) is 55 mm in diameter and the aperture is 26 mm in diameter. Our apparatus is an old Welch Scientific cat. no. 3552; most suppliers of instructional scientific apparatus sell some version of this. 2 E. Hecht and A. Zajac, Optics , (Addison-Wesley, Reading MA, 1974) pp 299-300 3 Alternatively, one can argue that the two reflections from the two surfaces cancel each other out because the second reflection (when light travels from air to glass) suffers a 180° phase shift. 4 For example, let's assume that the distance is exactly (1/4) λ for green (the center of the spectrum at 550 nm). The distance is thus 138 nm. This is 0.3 λ for blue (assuming 450 nm) and 0.21 λ for red (at 650 nm), both numbers being close to 0.25λ. 5 Logan model 2020 PortaView Light Box slide/transparency viewer; it measures approximately 45×35 cm. 6 Unilamp model UL-12, manufactured by Midwest Scientific Co., Sequal Manufacturing Inc., 3015 Power Drive, Kansas City, Kansas 66106; (913) 236-9674

Demo Subjects

Newtonian Mechanics Fluid Mechanics Oscillations and Waves Electricity and Magnetism Light and Optics Quantum Physics and Relativity Thermal Physics Condensed Matter Astronomy and Astrophysics Geophysics Chemical Behavior of Matter Mathematical Topics

Key to Catalog Listings

Size : from small [S] (benchtop) to extra large [XL] (most of the hall)  Setup Time : <10 min [t], 10-15 min [t+], >15 min [t++] /span> Rating : from good [★] to wow! [★★★★] or not rated [—] 

Complete key to listings

Newton’s ring experiment with animation

Newton’s ring is a process in which Circular bright and dark fringes obtained due to air film enclosed between a Plano-convex lens and a glass plate. An air wedge film can be formed by placing a Plano-convex lens on a flat glass plate. The thickness of the film is zero where the lens and the plate are in contact with each other. The thickness of the film gradually increases in all directions as we go away from the center.

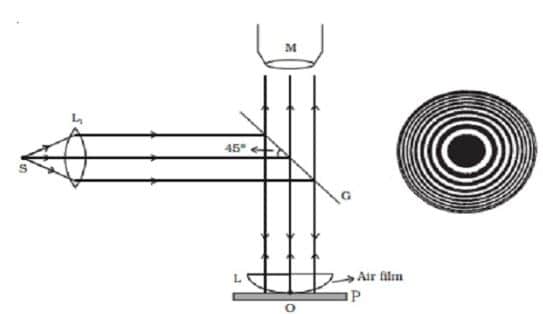
Experimental arrangement for newton rings experiment:

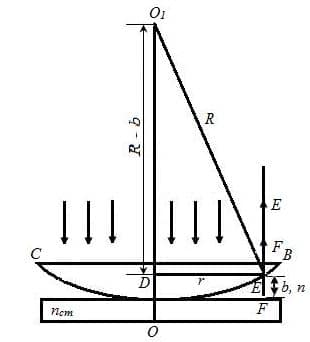
The experimental setup for Newton’s rings is shown in the figure. The light beam from source “S’ falls on the convex lens from where the rays become parallel and strike the glass plate ‘G’. The glass plate ‘G’ partly reflected the beam and partly refract toward the mirror. The mirror ‘M’ reflects back the beam towards the plano-convex lens. The thickness of air film between glass plate ‘P’ and plano-convex increases. For center ‘o’ to outwards. So at the point of contact, the path difference becomes ‘λ/2’ and destructive interference takes place. Similarly, when there is constructive interference the bright circular rings are seen. As a result, a series of dark or bright rings are seen, these are called newton’s rings.

Size of Newton rings:

Why newton rings are circular in nature?

Newton rings are circular in nature because the air film is symmetrical about the point of contact between the plano-convex lens and the glass plate. Newton’s ring experiment ( Video):

• https://en.wikipedia.org/wiki/Newton%27s_rings

Related Articles

Interference of light examples, properties of light in physics, what are the best types of binoculars to buy, examples of total internal reflection, leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

This site uses Akismet to reduce spam. Learn how your comment data is processed .